Ensembles de nombresetintervalles |
|
1°) Ensembles de nombres.1.1- Types de nombres.Il existe plusieurs types de nombres. Chaque type constitue un ensemble remarquable à part.1.2- Les ensembles.1.2.1-Les entiers naturels.Cet ensemble regroupe tous les entiers naturels positifs en plus du zéro (0). Exemple: 0, 1, 2, 3, …… 100, …, 1542 … Il existe une infinité d'entiers naturels. Cet ensemble est désigné par un n majuscule comme naturel.
Ces nombres naturels sont dits ainsi car ils sont naturellement utilisés au quotidien.
1.1.2-Les entiers relatifs.Cet ensemble regroupe tous les entiers négatifs, positifs et le zéro. Exemple: -102, -54, -10, 0, 25, 50, 200, … Il existe une infinité d'entiers relatifs. Cet ensemble est désigné par la lettre .
Cette désignation vient du mot allemand "die Zahl" qui signifie le nombre.
Donc d’après ce qui précède, il faut remarquer que tous les entiers naturels sont des entiers relatifs ce qui permet aussi de dire que l'ensemble est inclus dans l’ensemble . On note cette inclusion comme suit :
1.1.3-Les décimaux.Cet ensemble regroupe tous nombres dits "à virgule". Exemple: -2,33 et 15,2 sont des décimaux. Cet ensemble est désigné par la lettre .
Tous les entiers relatifs sont aussi des décimaux, car on peut leur ajouter des virgules suivi par un zéro. En effet :Exemple: 3 = 3,0 , 0 = 0,0 et -14 = -17,0 Comme les nombres entiers relatifs sont des nombres décimaux alors l'ensemble est inclu dans l’ensemble . Cette inclusion se note comme suit :
1.1.4-Les rationnels.Cet ensemble regroupe tous les nombres sous forme de fractions de la forme p/q où p et q sont des entiers (avec q <> 0). Exemple: 5/7 et -3/4. Cet ensemble des rationnels est désigné par la lettre pour quotient.
On remarque que les nombres décimaux peuvent être considérés comme des nombres rationnels.
Exemple:
225 est le quotient de 225 et 100 en effet 225/100 = 2.25.
Donc comme les entiers naturels sont des entiers relatifs et que les relatifs sont des décimaux et que les décimaux sont des rationnels alors on peut dire que les entiers naturels et les entiers relatifs sont des rationnels, ce qui se note comme suit :
1.1.5-Les réels.En géométrie, plusieurs problèmes ont conduit à la considération de nouveaux types de nombres comme les racines carrés, quelques constantes, √2, √3, … et autres, qui ne peuvent pas être des rationnels. Nous citons deux problèmes qui ont nécessités ces nouveaux types de nombres: a) La détermination de la longueur de l'hypoténuse d'un triangle rectangle isocèle de coté 1, h=1.√2 b) Le second est le périmètre d'un cercle de diamètre 1, p = 2 π R Ce qui a conduit à la création d’un ensemble regroupant tous les nombres mesurables et leurs opposés, cet ensemble est désigné par pour réel.
Un nombre réel est un nombre qui peut être représenté par une partie entière et une liste finie ou infinie de décimales.
L'ensemble des rationnels est donc inclus dans l’ensemble . On résume cela par :
Remarque:Un réel positif est un "nombre mesurable" qui peut être la longueur d’une ligne géométrique finie (c'est-à-dire un cercle, un segment ...). La longueur de n'importe quelle ligne géométrique finie est un nombre réel positif. D’où, la représentation possible de cet ensemble par une droite graduée dite, droite numérique, dont tous les points ont pour abscisse un nombre réel ou encore tout nombre réel est l'abscisse de l'un de ses points. Exemple: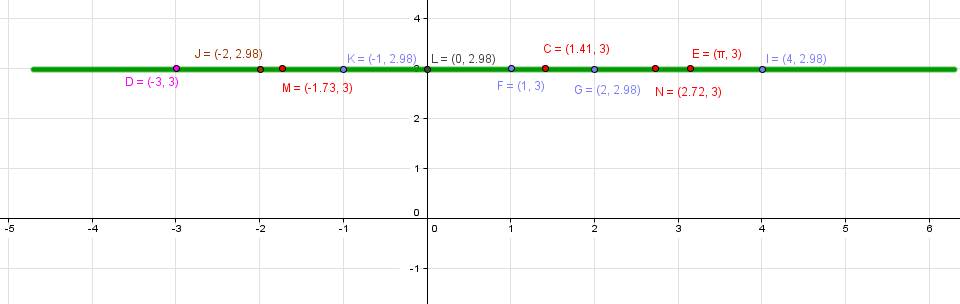
Sur ce graphique représentatif de la droite numérique on peut relever les abscisses des points représentées.
D a pour abscisse -3, ou encore 3 est l’abscisse du point D.
M a pour abscisse 1.73 ou encore -√3, ou encore -√3 est l’abscisse du point M.
F a pour abscisse 1, ou encore 1 est l’abscisse du point F.
C a pour abscisse 1.414 ou encore √2, ou encore √2 est l’abscisse du point C.
N a pour abscisse 2.72 ou encore e, ou encore e est l’abscisse du point N.
….
1.1.6-Les complexes. (Pour plus d’information voir les cours websavoir.net sur les nombres complexes)Les nombres complexes forment une extension de l'ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Un nombre complexe z se présente en général en coordonnées cartésiennes, comme une somme a + bi, où a et b sont des nombres réels quelconques et i (l’unité imaginaire) est un nombre particulier tel que i2 = –1. Le réel a est appelé partie réelle de z et se note Re(z) ou ℜ(z), le réel b est sa partie imaginaire et se note Im(z) ou ℑ(z). L'ensemble des sommes et produits de nombres réels et du nombre imaginaire i (les nombres de la forme a + ib) satisfait les propriétés d'une structure de corps commutatif qui contient le corps des réels. Cet ensemble des nombres complexes est désigné par la lettre pour complexe.
Comme cet ensemble constitue une extension de alors on peut écrire ce qui suit :
2°) Intervalles réels.On peut dire que les intervalles réels sont des sous-ensembles inclus dans l'ensemble des réels. Ils se caractérisent par leur "continuité", ou en d'autre termes, le chemin enprunté pour passer d'un élément à un autre élément tout deux appartenant au même intervalle est dans cet intervalle. Ils sont représentés sur la droite numérique par des segments ou des droites dont les extrémités peuvent être incluses ou exclues, d'ou l'appellation, intervalle ouvert et intervalle fermé. Dans le tableau ci-dessous, a et b sont deux réels tels que a ≤ b.  |
|
 |
||||||||||